On the 6th July 2020, enclosing notes written by
Joachim Brügge,
Awani Kumar sent an e-mail to our circle of magic square enthusiasts, asking whether a bimagic queen's tour might exist on an 8 x 8 or larger board, and invited us to "settle the question." I was intrigued by this interesting challenge, and after a first analysis of Joachim Brügge's approach, and exchanging e-mails with him, I decided to search for a solution.
Some Important Definitions
A standard chess board is an 8 x 8 square grid upon which the queen can move any number of squares, either orthogonally, or along ± 1 / ± 1 diagonals. A queen's tour is a sequence of queen's moves in which she visits each of the 64 squares once. If the queen ends her tour on a square which is at a single queen's move from the starting square, the tour is closed; otherwise the queen's tour is open. Here it is useful to clarify the definition of a
bimagic queen's tour, which is
different to that of a bimagic square: In chess literature, as confirmed by
George Jelliss, the term
magic is commonly used for all tours in which the successively numbered positions of the chess piece in each rank and file add up to the same orthogonal total (the magic constant S1), and should the entries on the two long diagonals also add up to the same magic constant, the tour is deemed to be diagonally magic. (In fact, it is now known, thanks to the work of
G. Stertenbrink, J-C. Meyrignac and H. Mackay, who have completed the list of all of the 140
magic knight tours on an 8 x 8 board, that none of these have two long magic diagonals). Extending the above definition of a magic tour to that of a
bimagic queen's tour, not only the successively numbered positions of the queen in each rank and file should add up to a same orthogonal total
(the magic constant S1), but also the
squared entries of each rank and file should add up to an additional total which is
the bimagic constant S2.
For a N x N board, when N = 8, the magic constant S1 = 260.
For a N x N board, when N = 8, the bimagic constant S2 = 11180.
More information about how the magic and bimagic constants are calculated can be found in the website of
Christian Boyer.
The First Hypotheses
Before beginning the search for a solution to the bimagic queen's tour question, the following hypotheses were considered:
Firstly, it seemed logical to privilege diagonal queen moves that would be less likely to perturb the orthogonal bimagic series of the ranks and files.
Secondly, it seemed pertinent to make selections from the 240 immutable bimagic series of order-8; series named this way by
Dwane Campbell, who identified and listed these some years ago. 192 of these series have the advantage of having a regular distribution, with each of their eight numbers coming from different eighths of the sequence 1 to 64.
Thirdly, it seemed probable that by using symmetric arrays of bimagic series, this would be beneficial for overall balance, and increase the chances of success.
The First Trials and Observations
Although I was at first unable to find a complete bimagic queen's tour, testing the above hypotheses gradually produced encouraging results. On the 18th July I was able to write an e-mail to Joachim Brügge announcing that I had found several broken bimagic queen's tours, with 4, 3, and even 2 separate sequences.
In all of these broken tours, because of the characteristics of the bimagic series that were tested, the sequence breaks occurred precisely at certain junctions between the different quarters of N², and it was of utmost importance to find a regular sequence that could negotiate these obstacles with valid diagonal queen's moves.
Also during these early trials I noticed that when certain diagonal moves "exited" the board they "re-entered" it in cells that were no longer directly accessible to the queen. The following diagram shows how this occurs:
 |
| How certain diagonal moves break the queen's tour |
In order to improve the chances of success of a queen's tour, which was necessarily limited to the board, I realised it would be best to use ± N/2, ± N/2, i.e. ± 4, ± 4 diagonal queen's moves as illustrated below. The advantage of such moves was that when they "left" the board they always "re-entered" it in cells that the queen could once again access, even if along an alternative diagonal.
 |
| ± N/2, ± N/2 diagonal moves never break the queen's tour |
In order to optimise the ``convergence" effect of these ± N/2, ± N/2 i.e. ± 4, ± 4 diagonals, they should be used once every two moves.
Despite the inconvenience of their spreading beyond the edges of the board, a large use of ± 2, ± 2 diagonal moves often produced complete, though irregular bimagic queen's tours, such as the one below, observed on the limitless surface of a
semi-bimagic torus:
 |
| An open queen's tour on a torus board |
The First Bimagic Queen's Tour
Finally, on the 23rd July 2020, after revising the selection of immutable bimagic series, the following method proved to be successful:
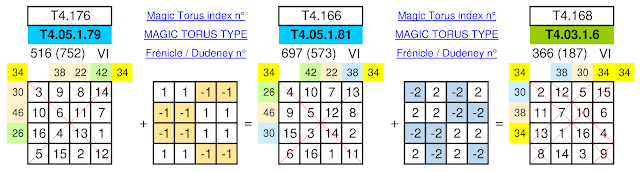
The tables below are
doubly-symmetric arrays of immutable bimagic series, specially created for the x and y coordinates of a suitable
semi-bimagic torus. Arranged in groups of four, the eight colours that represent the x (file) and y (rank) coordinates can be freely attributed the values of 0 to 7:
 |
| Tables of coordinates for the Bimagic Queen's Tour Torus |
However, to construct a bimagic tour we need a regular sequence that satisfies the ±1 / ±1 diagonal constraints of regular queen's moves, and in order to make the queen's tour "converge" on the board we need to use as many ± 4, ± 4 diagonals as we can; the optimum being once every two moves. Additionally, we need to check that the x and y coordinates selected for the first eight positions of the queen will also allow for regular diagonal transitions between each quarter of N² at the moves 16-17, 32-33 and 48-49... Once these verifications are complete we can then use the approved coordinates to plot the successive positions of the queen on the semi-bimagic torus shown below, starting with the first position 1 at coordinates (0x, 0y) in the lower left-hand corner:
 |
| The Semi-Bimagic Torus Before Translation |
When constructed, the semi-bimagic torus appears to only contain a broken tour; but after a translation of the 8 x 8 board viewpoint, as shown below, a complete open bimagic queen's tour is revealed:
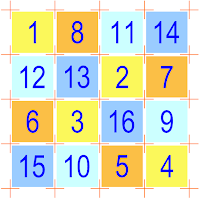
 |
| The First Bimagic Queen's Tour |
Displaying beautiful symmetries, this is apparently not only the first bimagic queen's tour, but also the first-known bimagic tour of any chess piece!
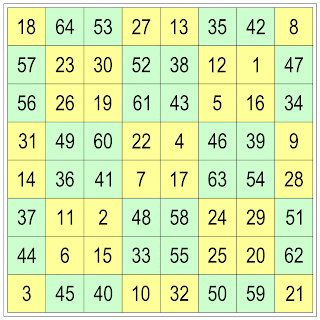
In each rank and file, the orthogonal total of the successively numbered positions of the queen is the magic constant S1 = 260, and (as can be verified in the squared version below), the orthogonal total of the squares of the successively numbered positions of the queen is the bimagic constant S2 = 11180.
 |
| The Squared Bimagic Queen's Tour |
Observing the bimagic queen's tour path we can see the symmetries of the four orthogonal moves (8 - 9, 24 - 25, 40 - 41, and 56 - 57). Thirty-two out of the sixty-three queen's moves are ±4, ±4 diagonal.
 |
| The Bimagic Queen's Tour Path |
Conclusion
It is probable that many other examples exist, and that these will include closed bimagic queen's tours. However, it is an open question as to whether or not a
diagonally bimagic queen's tour can be found on an 8 x 8 board! *
For those who are interested, a PDF file of "A Bimagic Queen's Tour" can be downloaded
here.
Latest Developments!
The Answer to the Open Question!
On the 3rd August 2020,
Walter Trump was already able to answer the "open question" that I had formulated in my conclusion! He ran a computer check on the complete set of bimagic 8x8 squares that he had previously found with
Francis Gaspalou. Walter found that
on an 8x8 board there are no diagonally bimagic queen's tours (or diagonally bimagic knight's tours for that matter, although it was already known that none of the 140 magic knight's tours were diagonally magic)
. The longest possible queen's tour on a bimagic square of order-8 consists of 21 moves, as illustrated in his PDF file below:
106 Bimagic Queen's Tours on an 8x8 Board!
On the 8th August 2020, testing a program that he had devised on the first bimagic queen's tour, Walter Trump found a second example, which turned out to be a complementary bimagic queen's tour. On the 11th August 2020, continuing to search with his program, Walter Trump was able to find a total of 44 closed and 62 open bimagic queen's tours!
Walter Trump conjectures that, up to symmetry, there are no further bimagic queen's tours to be found on an 8x8 board. The program searched within the semi-bimagic 8x8 squares which were found by Walter Trump and Francis Gaspalou in 2014. Essentially different means up to symmetry and permutations of rows and columns. Unique means up to symmetry. Considering that there are more than 715 quadrillion unique semi-bimagic squares of order-8, the 106 unique queen's tours are quite rare!
Other Publications about Bimagic Queen's Tours!
In a German book co-authored with
Hans Gruber, entitled
"Schach als Sujet in den Künsten und der Wissenschaft", and published on the 1st April 2022,
Joachim Brügge has included a chapter "Die erste Darstellung einer semi-bimagischen Damenwandering von William Walkington (2020)." The chapter relates the discovery of the first bimagic queen's tour, and also that of the other bimagic queen's tours on an 8x8 board which were later found by Walter Trump.
Acknowledgements
I am indebted, not only to
Awani Kumar, for initially bringing the subject to our attention and for his appeal for a solution, but also to
Joachim Brügge, for having had the idea of a bimagic queen's tour in the first place, and for his kind encouragements during my research.
My thanks also go to
Dwane Campbell, for publishing his findings on immutable bimagic series; series which proved so useful in the search for the bimagic queen's tour. Dwane has informed me that
Aale de Winkel was the first to recognize that component binary squares could be bimagic, the basis of immutable series; so my thanks to Dwane go indirectly to Aale as well.
I am also most grateful to
Francis Gaspalou, for editing and sending our circle of magic square enthusiasts an
"Analysis of the 240 Immutable Series of order 8" in 2018, and for sending me the full list of all 38 069 bimagic series of order-8 when I asked him for information about these in July this year.